DERIVADAS Este programa trata de derivadas. O programa contém instruções que devem ser vistas para utilizá-lo corretamente e comentários onde se dão sugestões para a sua aplicação. Nas imagens seguintes dá-se uma ideia do que se pode fazer com este programa. |
|
Este programa foi construido tanto para os professores utilizarem nas suas aulas, como para os alunos melhorarem a compreensão dos vários temas em suas casas. Os conceitos que se podem estudar são o de tangente a uma linha, derivada de uma função num ponto, função derivada, relação entre função, primeira derivada e segunda derivada, etc. Há páginas para as definições e compreensão e outras onde os utilizadores poderão escrever as expressões analíticas das funções que desejarem estudar. As animações na janela de desenho ajudam a compreensão dos vários conteúdos. |
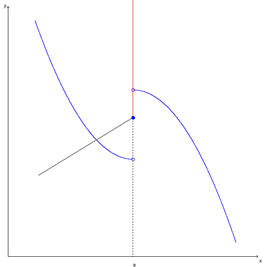
| Na
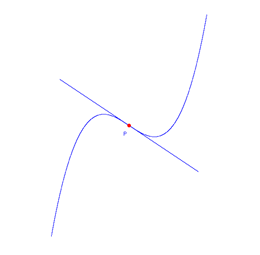
primeira página introduz-se o conceito de derivada. Por meio de animações, começa-se por mostrar o caso geral de tangente a uma linha num ponto a partir das semi-secantes à esquerda e à direita. Depois, ainda com animações, passa-se às derivadas e derivadas laterais. |
 |
 |
 |
 |
 |
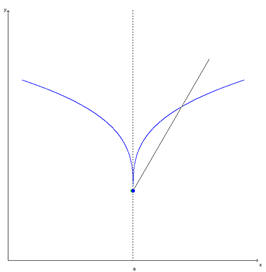 |
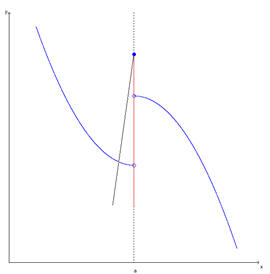
É estudada também a existência de derivada ou derivadas laterais em pontos de descontinuidade e em pontos especiais. |
|
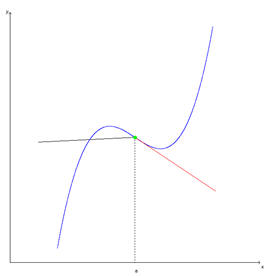
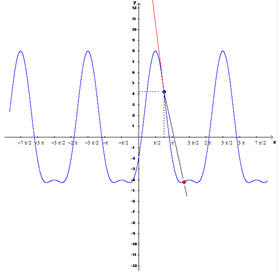
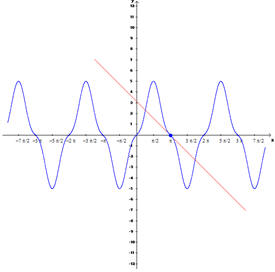
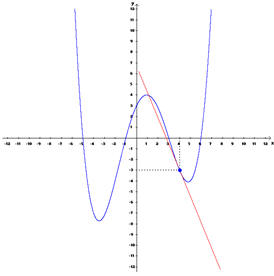
Finalmente, existe a página onde o utilizador escreve a expressão da função e na janela de desenho é mostrado o gráfico. Seguidamente escolhe-se a abcissa do ponto e o programa mostra analítica e graficamente o valor da derivada. |
 |
 |
 |
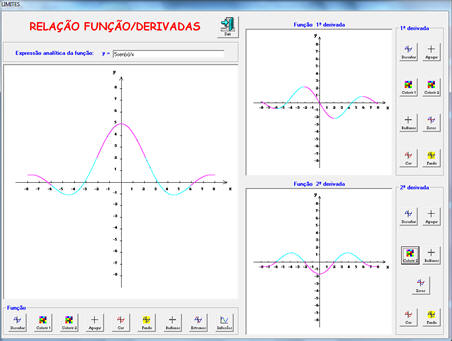 |
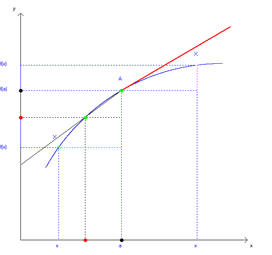
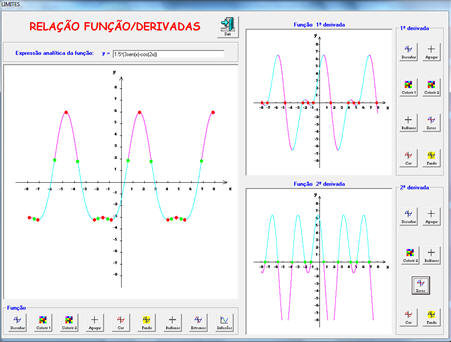
Nas
derivadas podem ver-se as relações existentes entre uma função e
as suas primeira e segunda derivadas. Essas relações ficam mais visíveis por ser possível utilizar cores para representar os pontos e intervalos correspondentes nos três gráficos. |
 |
|
NOTA
IMPORTANTE |
|
Descarregar o Derivadas.zip (4345 KB) Versão 1.0 Para instalar, descomprima o zip, abra o ficheiro Package e execute o SETUP. É conveniente criar antes uma pasta com o nome Derivadas e mandar o setup fazer a instalação para lá. |